In this post, I will introduce a Reinforcement Learning (RL) algorithm based on an “alternative” model: Divide and conquer. Unlike traditional methods, this algorithm no Based on time-difference (TD) learning (which Scalability challenges), and suits well for long-range missions.
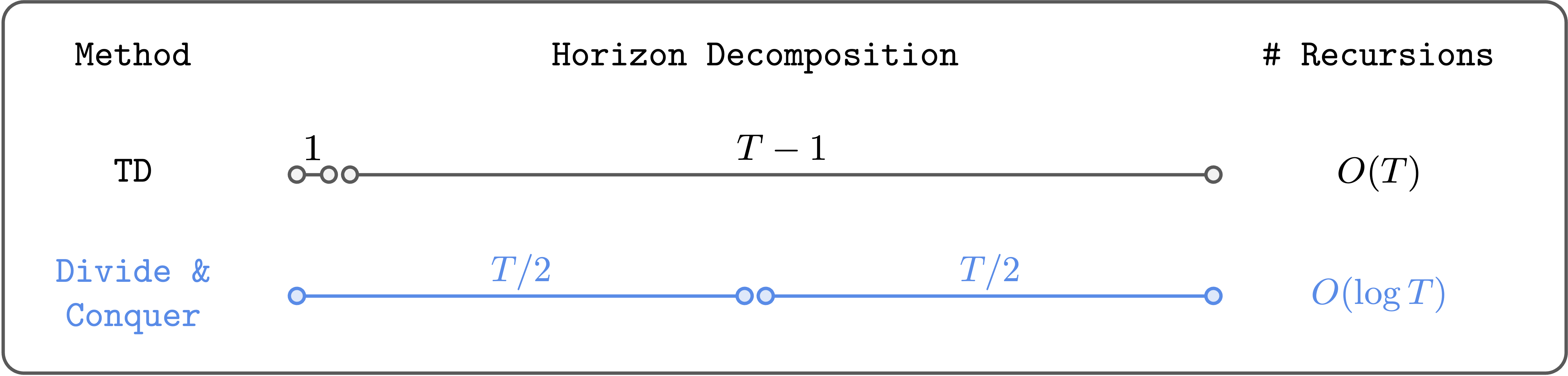
We can do reinforcement learning (RL) on a divide-and-conquer basis, rather than temporal difference (TD) learning.
Problem setting: RL is out of policy
Our problem situation is Outside politics RL. Let’s briefly review what this means.
There are two categories of algorithms in RL: on-policy RL and off-policy RL. At the policy level RL means we can only Use new data collected by existing policy. In other words, we have to get rid of old data every time we update the policy. Algorithms such as PPO and GRPO (and political gradient methods in general) belong to this category.
RL outside the policy means we don’t have this restriction: we can use it any Data type, including historical experience, human demos, Internet data, etc. So off-policy RL is more general and flexible than off-policy RL (and of course harder!). Q-learning is the most well-known RL algorithm outside politics. In areas where data collection is expensive (For example, Robotsdialogue systems, health care, etc.), we often have no choice but to use RL outside of politics. That’s why it’s an important problem.
As of 2025, I think we have reasonably good recipes for scaling up knowledge-based policy (For examplePPO, GRPO, and their variants). However, we have not yet been able to find “scalability”. Outside politics RL The algorithm adapts well to complex and long-horizon tasks. Let me briefly explain why.
Two models in value learning: time difference (TD) and Monte Carlo (MC)
In off-policy RL, we typically train the value function using temporal difference (TD) learning.anyQ-learning), with the following Bellman update rule:
\(\begin{align} Q(s, a) \gets r + \gamma \max_{a’} Q(s’, a’), \end{align}\)
The problem is as follows: the error in the next value $Q(s’, a’)$ propagates to the current value $Q(s, a)$ through preamble, and these errors Accumulate Over the entire horizon. This is essentially why TD learning struggles to scale to long-term tasks (see this post If you are interested in more details).
To mitigate this problem, people mix TD learning with Monte Carlo (MC) returns. For example, we can perform TD $n$-step (TD-$n$) learning:
\(\begin{aligned} Q(s_t, a_t) \gets \sum_{i=0}^{n-1} \gamma^i r_{t+i} + \gamma^n \max_{a’} Q(s_{t+n}, a’). \end{aligned}\)
Here, we use the actual Monte Carlo returns (from the dataset) for the first $n$ steps, and then use the bootstrap value for the rest of the horizon. In this way, we can reduce the number of Bellman iterations by $n$ times, and thus accumulate fewer errors. In the extreme case $n = \infty$, we recover pure value Monte Carlo learning.
While this is a reasonable (and often… It works fine), which is highly unsatisfactory. First, it doesn’t happen Basically Solve the problem of accumulating errors. It only reduces the number of Bellman iterations by a constant factor ($n$). Second, as $n$ grows, we experience high variance and low optimality. So we can’t just set $n$ to a large value, we need to adjust it carefully for each task.
Is there a radically different way to solve this problem?
The “third” model: divide and conquer
My claim is that A third model for learning value, Divide and conquermay provide an optimal solution for off-policy RL that is suitable for arbitrarily long-running tasks.
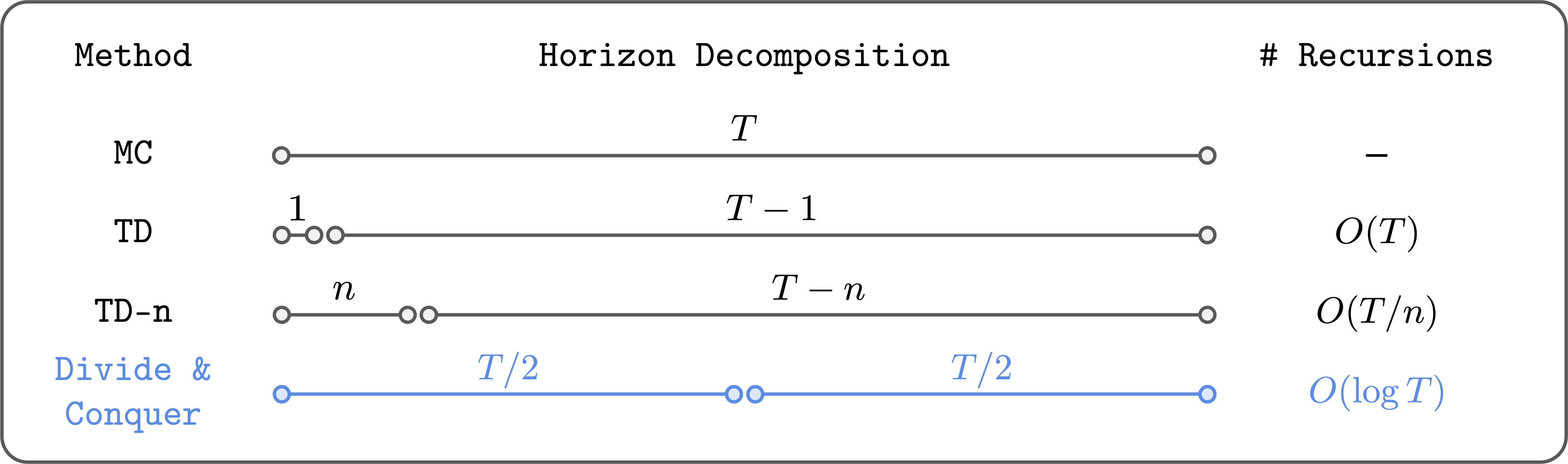
Divide and conquer logarithmically reduces the number of Bellman iterations.
The basic idea of the divide and conquer policy is to divide the path into two parts of equal length, and merge their values to update the value of the complete path. In this way, we can (theoretically) reduce the number of Bellman iterations Logarithmically (Not linear!). Moreover, it does not require hyperparameter selection such as $n$, and does not necessarily suffer from high or suboptimal variance, unlike $n$-step TD learning.
In theory, divide and conquer has all the great properties we want in value learning. I’ve long been excited about this high-level idea. The problem was that it wasn’t clear how to do this in practice…until recently.
Practical algorithm
In a Last work In association with AdityaWe have made significant progress towards realizing and scaling this idea. Specifically, we were able to extend divide-and-conquer value learning to very complex tasks (to my knowledge, this is the first work of its kind!) in at least one important class of RL problems, RL conditioned to the target. Objective-conditional RL aims to learn a policy that can reach any state from any other state. This provides a natural divide and conquer structure. Let me explain this.
The structure is as follows. Let us first assume that the dynamics are deterministic, and denote the shortest path distance (“time distance”) between two states $s$ and $g$ as $d^*(s, g)$. Then he satisfies the triangle inequality:
\(\begin{align} d^*(s, g) \leq d^*(s, w) + d^*(w, g) \end{align}\)
For all $s, g, w \in \mathcal{S}$.
In terms of values, we can translate this triangle inequality equivalently into the following “transitive” Bellman update rule:
\begin{aligned} V(s, g) \gets \begin{cases} \gamma^0 & \text{if } s = g, \\\\ \gamma^1 & \text{if } (s, g) \in \mathcal{E}, \\\\ \max_{w \in \mathcal{S}} V(s, w)V(w, g) & \text{otherwise} \end{states} \end{alignment}\)
where $\mathcal{E}$ is the set of edges in the transition graph of the environment, and $V$ is the value function associated with the sparse reward $r(s, g) = 1(s = g)$. Intuitivelythis means that we can update the value of $V(s, g)$ using two “smaller” values: $V(s, w)$ and $V(w, g)$, provided that $w$ is the ideal “midpoint” (sub-goal) on the shortest path. This is exactly the divide-and-conquer value update rule we’ve been looking for!
The problem
However, there is one problem here. The problem is that it is not clear how to choose the optimal subgoal $w$ in practice. In tabular settings, we can simply enumerate all states to find the optimal $w$ (this is essentially the Floyd-Warshall shortest path algorithm). But in continuous environments with large state areas, we cannot do this. Essentially, this is why previous work has struggled to extend divide-and-conquer value learning, even though this idea has been around for decades (in fact, dating back to the first work on goal-conditioned learning by Killbling (1993) – He sees Our paper For further discussion of related works). The main contribution of our work is the practical solution of this issue.
the solution
This is our main idea: WE restricts The search space $w$ refers to instances that appear in the data set, specifically those that lie between $s$ and $g$ in the data set path. Also, instead of searching for the optimal $\text{argmax}_w$, we compute the “smooth” $\text{argmax}$ using Expected regression. That is, we reduce the following loss:
\(\begin{aligned} \mathbb{E}\left(\ell^2_\kappa (V(s_i, s_j) – \bar{V}(s_i, s_k) \bar{V}(s_k, s_j))\right), \end{aligned}\)
where $\bar{V}$ is the target value network, $\ell^2_\kappa$ is the expected loss with $\kappa$ expected, and the forecast is taken over all sets $(s_i, s_k, s_j)$ with $i \leq k \leq j$ in the path of a randomly sampled data set.
This has two benefits. First, we do not need to search the entire country. Second, we prevent overestimation from the $\max$ operator by using the “softer” expected regression instead. We call this algorithm transitive RL (TRL). Payment Our paper More details and more discussions!
Does it work well?
com. humanoidmaze
puzzle
To see if our method scales well with complex tasks, we directly evaluated TRL on some of the most challenging tasks in Ogbenchwhich is a benchmark for offline target-adapted RL. We mainly used the most difficult versions of human maze and puzzle tasks with 1B large datasets. These tasks are very challenging: they require the performance of combinatorially complex skills across up to 3000 eco-steps.
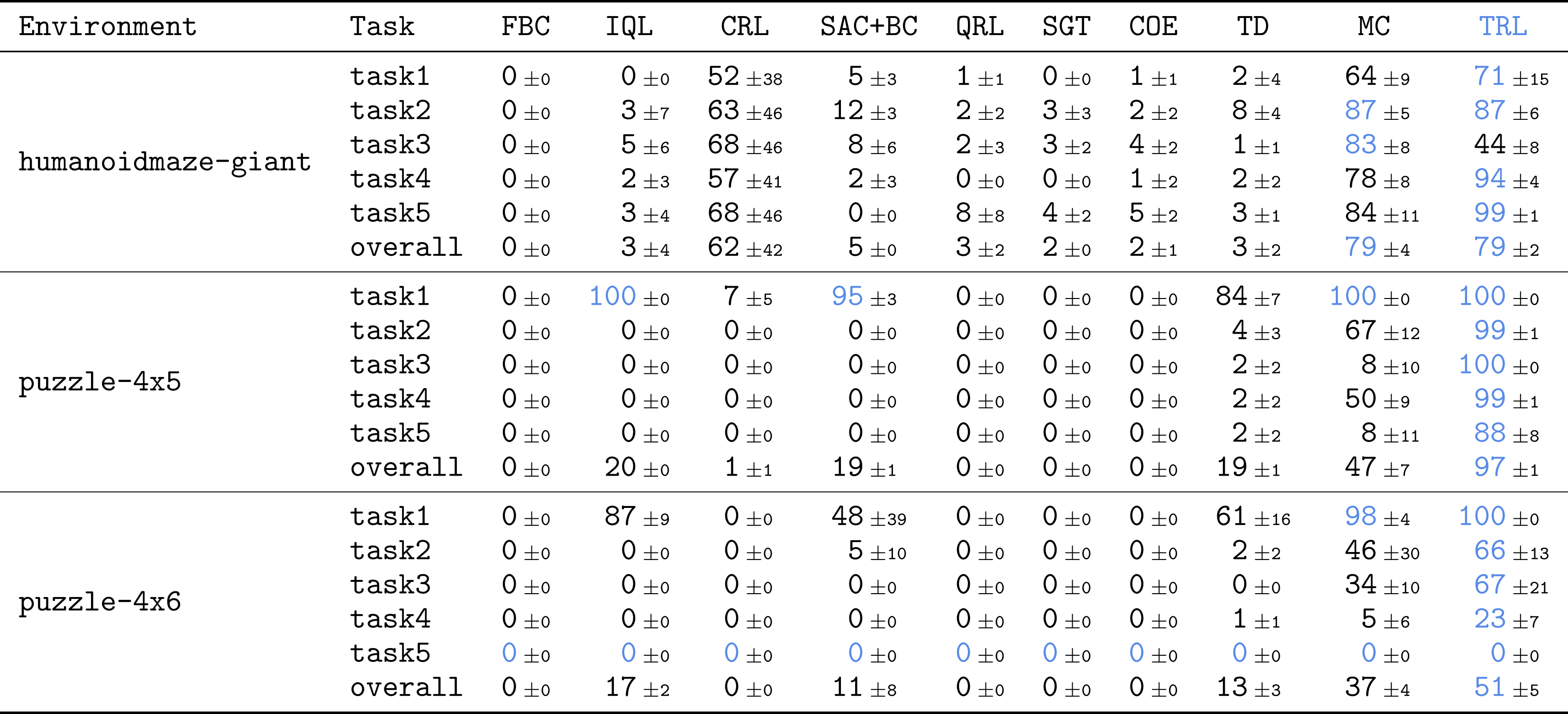
TRL performs best on very challenging, long-horizon missions.
The results are very exciting! Compared to several robust baselines across different categories (TD, MC, semi-metric learning, etc.), TRL achieves the best performance on most tasks.
TRL matches the best individually tuned TD-$n$, Without having to set $\boldsymbol{n}$.
This is my favorite plot. We compare TRL with $n$-step TD learning at different values of $n$, from $1$ (pure TD) to $\infty$ (pure MC). The result is really beautiful. TRL matches the best TD-$n$ in all tasks, Without having to set $\boldsymbol{n}$! This is exactly what we wanted from the divide and conquer model. By repeatedly dividing the path into smaller paths, this can be achieved Naturally Handle long horizons, without having to arbitrarily choose the path cutting length.
The paper contains a lot of additional experiments, analyzes and excerpts. If you’re interested, check it out Our paper!
What’s next?
In this post, I share some promising results from a new divide-and-conquer value learning algorithm, Transitive RL. This is just the beginning of the journey. There are many open questions and exciting directions to explore:
-
Perhaps the most important question is how to extend TRL to normal reward-based RL tasks beyond goal-conditioned RL. Would regular RL have a similar divide-and-conquer structure that we could exploit? I’m very optimistic about this, since any reward-based RL task can be converted into a goal-conditioned task at least in theory (see page 40 of This book).
-
Another important challenge is dealing with random environments. The current version of TRL assumes deterministic dynamics, but many real-world environments are stochastic, mainly due to partial observability. For this, Inequality in a “random” triangle. It may provide some hints.
-
In practice, I think there is still a lot of room to improve TRL further. For example, we can find better ways to select candidates for subgoals (other than those belonging to the same path), further reduce hyperparameters, increase training stability, and further simplify the algorithm.
Overall, I’m really excited about the potential of the divide and conquer model. I Still I think one of the most important problems in RL (and even in machine learning) is finding Scalable The RL algorithm is outside the policy. I don’t know what the final solution would look like, but I think divide and conquer, or Recursion Decision making, in general, is one of the strongest candidates for achieving this holy grail (by the way, I think other strong contenders are (1) model-based learning and (2) TD learning with some “magic” tricks). In fact, several recent works in other fields have shown the promise of iteration and divide-and-conquer strategies, e.g Abbreviation forms, Linear attentionand Recursive language models (And of course, classic algorithms like quicksort, segment trees, FFT, etc.). I hope to see more exciting progress in scalable RL outside of politics in the near future!
Thanks and appreciation
I would like to thank Kevin and Sergey For their helpful feedback on this post.
This post originally appeared on Sihong Park’s blog.